V nadaljevanju je predstavljen del teorije, ki se nanaša na izjavno logiko, množice in računanje z množicami. Izjavna logika je ena izmed mnogih vej logike, ki so se razvile skozi čas. Od ostalih se razlikuje po svojem sistemu znakov in pravil.

Med razlago najdeš tudi rešene primere in naloge s katerimi lahko preizkusiš svoje znanje.

IZJAVE IN IZJAVNE POVEZAVE

Izjava je trditev, za katro lahko določimo, ali je pravilna ali nepravilna.
Pravimo, da ji določimo njeno logično vrednost.
Izjave običajno označujemo z velikimi črkami A, B…, logične vrednosti pa s p ali 1, če je izjava pravilna in n ali 0, če je izjava napačna.

Ločimo dve skupini izjav.
Elementarne izjave so tiste, ki jih ne moremo razstaviti na bolj enostavne.
Sestavljene izjave pa so tiste izjav, ki jih sestavimo iz elementarnih izjav s pomočjo izjavnih povezav.

Poznamo 5 različnih izjavnih povezav (negacija, konjunkcija, disjunkcija, implikacija in ekvivalenca), ki so predstavljene v nadaljevanju.

NEGACIJA

Negacija izjave A je izjava, ki trdi nasprotno kot izjava A.

Simbol za negacijo je ¬ .

¬A … NI RES, da velja A

Negacija negacija: ¬(¬A) = A

Tabela izjavnih vrednosti:

A	¬A
1	0
0	1

2. KONJUNKCIJA

Konjunkcija izjav A in B nastane kadar hkrati veljata izjavi A in B.

Simbol za konjunkcijo je ∧.

A ∧ B … velja A IN HKRATI velja B

Za izjavno povezavo konjunkcija velja:

- komutativnost (A ∧ B = B ∧ A)
- asociativnost ((A ∧ B) ∧ C = A ∧ (B ∧ C))

Tabela izjavnih vrednosti:

A	B	*A ∧ B*
1	1	1
1	0	0
0	1	0
0	0	0

3. DISJUNKCIJA

Disjunkcija izjav A in B nastane kadar velja A ali B.

Simbol za disjunkcijo je ∨.

A ∨ B … velja A ALI velja B

Za izjavno povezavo disjunkcija velja:

- komutativnost (A ∨ B = B ∨ A)
- asociativnost ((A ∨ B) ∨ C = A ∨ (B ∨ C))
- distributivnost ((A ∨ B) ∧ C = (A ∧ C) ∨ (B ∧ C) in (A ∧ B) ∨ C = (A ∨ C) ∧ (B ∨ C) )

Tabela izjavnih vrednosti:

A	B	*A ∨ B*
1	1	1
1	0	1
0	1	1
0	0	0

4. IMPLIKACIJA

Implikacija izjav je sestavljena izjava, kjer je izjava A pogoj in izjava B posledica izjave A.

Simbol za implikacijo je ⇒.

A ⇒ B … iz A SLEDI B

(zapis lahko beremo tudi kot, če velja A, potem velja B ali velja B pri pogoju, da velja A)

Tabela izjavnih vrednosti:

A	B	A ⇒ B
1	1	1
1	0	0
0	1	1
0	0	1

5. EKVIVALENCA

Ekvivalenca izjav A in B je izjava, ki je pravilna, samo kadar sta izjava A in izjava B po vrednosti enaki (obe hkrati pravilni ali obe hkrati napačni).

Simbol za ekvivalenco je ⇔.

A ⇔ B … velja A NATANKO TEDAJ, ko velja B

(zapis lahko beremo tudi kot, velja A če in samo če velja B)

Tabela izjavnih vrednosti:

A	B	A ⇔ B
1	1	1
1	0	0
0	1	0
0	0	1

Med prebiranjem zapisov z logično vsebino, lahko veliko krat zasledimo naslednje izraze:

- Izjavi A in B sta ENAKOVREDNI ali EKVIVALENTNI (A = B) natanko tedaj, ko imata pri vsakem naboru logičnih vrednosti osnovnih izjav enako končno logično vrednost.

- TAVTOLOGIJA je izjava, ki je vedno pravilna (pri vsakem naboru logičnih vrednosti osnovnih izjav).

- Izjavi, v kateri trdimo med seboj nasprotne stvari, pravimo PROTISLOVNA IZJAVA oziroma PROTISLOVJE.

REŠENA NALOGA (preverjanje razumevanja izjavnih povezav)

Za izjavo (A⇒ B) ⇔ (¬A∨ B), dopolni tabelo.

A	B	¬A	¬A∨ B	A⇒ B	(A⇒ B) ⇔ (¬A∨ B)
1	1	0	1	1	1
1	0	0	0	0	1
0	1	1	1	1	1
0	0	1	1	1	1

Vrstni red operatorjev

Če v izjavi ne nastopajo oklepaji, si izjavne povezave po pomembnosti sledijo v naslednjem vrstnem redu: ¬, ∧, ∨, ⇒, ⇔ . Sicer vrstni red operatorjev določajo oklepaji.

Če v izjavi nastopajo trije ali več zaporednih enakih operatorjev, izjave rešujemo od leve proti desni.

MNOŽICE IN RAČUNANJE Z MNOŽICAMI

Množica je poljubna skupina elemenov.

Množico lahko zapišemo z

- naštevanjem elementov med zavite oklepaje {} (npr. {1,2,3,4});
- uporabo zapisa z lastnostjo (npr. {n; (n ∈ ℕ) ∧ (n ≤ 6)}={1, 2, 3, 4, 5, 6});
- zapisom s formulo (npr. {2k; k ∈ ℕ} = {2, 4, 6, …}).

Če je a element množice A označimo z a ∈ A. Če a ni element množice A označimo a ∉ A.

Prazno množico označimo z {} ali Ø .

MOČ MNOŽICE

Moč množice je število elementov dane množice. Označimo jo z m(A).

Zgledi:

A = {1, 2, 3, 4} … m(A) = 4

B = {2, 4, 6, 8, 10, 12} … m(B) = 6

Dve množici z enako močjo sta EKVIPOLENTNI množici.

Množica A = {1, 2, 3, 4} in množica B = {20, 49, 59, 100} sta ekvipolentni množici, saj sta njuni moči enaki (m(A) = m(B)).

PODMNOŽICA

Množica A je podmnožica množice B, če je vsak element množice A tudi element množice B.

Oznaka: A ⊂ B

Matematični zapis: A ⊂ B ⇔ (∀ x ∈ A ⇒ x ∈ B)

Dve množici sta si enaki če velja naslednje: A = B ⇔ ((A ⊂ B) ∧ (B ⊂ A))

UNIVERZALNI KVANTIFIKATOR: ∀

beremo … za vsak

∀ x : L … za vsak x velja L

EKSISTENCIALNI KVANTIFIKATOR: ∃

beremo … obstaja

∃ x : L … obstaja x, da velja L

POTENČNA MNOŽICA

Potenčna množica množice A je množica vseh podmnožic množice A.

Oznaka: P(A)

Matematični zapis: P(A) = {X, X ⊂ A}

Moč potenčne množice: m(P(A)) = 2^(m(A))

Zgled:

Naj bo A = {1, 2, 3}. Določi potenčno množico množice A ter m(A) in m(P(A)).

Potenčna množica množice A: P(A) = {{}, {1}, {2}, {3}, {1, 2}, {1, 3}, {2, 3}, {1, 2, 3}}

Moč množice A: m(A) = 3

Moč potenčne množice množice A: m(P(A)) = 2³ = 8

KOMPLEMENT MNOŽICE

Komplement množice A je množica, ki vsebuje tiste elemente univerzalne množice, ki niso vsebovani v množici A.

Oznaka: A^C

Matematični zapis: A^C= {x; x ∉ A}

Komplement komplementarne množice je množica sama: A = (A^C)^C

UNIJA MNOŽIC

Unija množice A in mnižice B je množica, ki vsebuje vse elemente iz obeh množic.

Oznaka: ∪

Matematični zapis: A ∪ B = {x; (x ∈ A) ∨ (x ∈ B)}

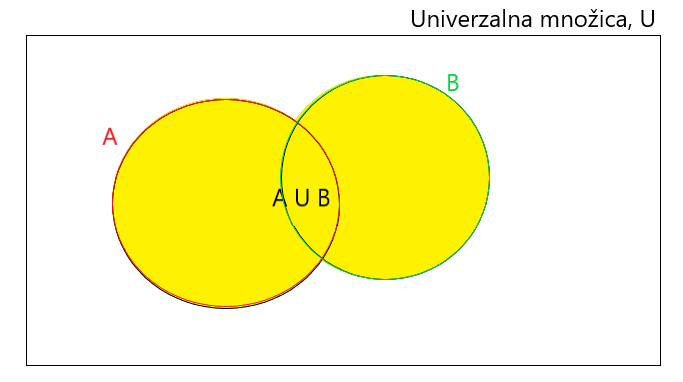
Unija by PeharcL is licensed under CC BY-NC-SA 4.0

PRESEK MNOŽIC

Presek množice A in množice B je množica, ki vsebuje vse elemente, ki so hkrati v množici A in v množici B.

Oznaka: ∩

Matematični zapis: A ∩ B= {x; (x ∈ A)∧(x ∈ B)}

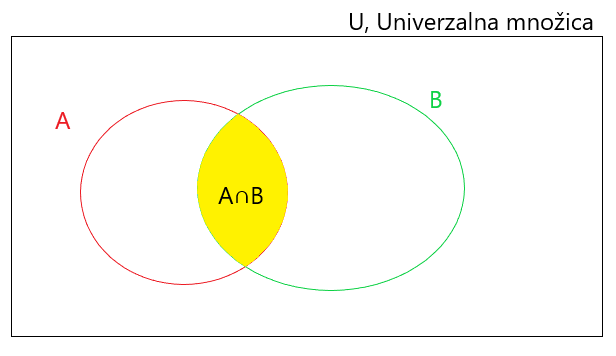
Presek by PeharcL is licensed under CC BY-NC-SA 4.0

RAZLIKA MNOŽIC

Razlika množic A in B je množica sestavljena iz elementov, ki pripadajo množici A in hkrati ne pripadajo množici B.

Oznaka: A \ B ali A − B

Matematični zapis: A \ B = {x; (x ∈ A) ∧ (x ∉ B)}

Zgled:

Naj bo A = {1, 2, 3, 4} in B = {3, 4, 5, 6}. Zapiši A\B in B\A.

A\B = {1, 2}

B\A = {5, 6}